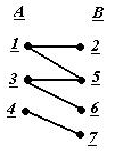Terminologie:
- Se numeste nod terminal un nod care are gradul egal cu 1.
- Se numeste nod izolat un nod care are gradul 0
X={1,2,3,4,5,6}
U={(1,2),(1,6),(2,6),(3,5)}
nodurile 1 si 2 sunt nodurile vecine nodului 6;
nodurile 5 si 3 sunt noduri terminale;
nodul 4 este nod izolat.
Exemplu:
- Multimea nodurilor: X={1,2,3,4,5,6,7}
- Multimea muchilor: U={(1,2), (2,3), (2,4), (3,4), (5,6)}
- Gradul nodului 2: d(2)=3
- Nodu izolat: 7
- Noduri terminale: 1, 5, 6
- Nodurile 2 si 3 se numesc adiacente. La fel nodurile 2 si 4.
- Nodul 2 si muchia (3,4) se numesc incidente.
Teoreme:
1.Numarul total de grafuri cu n noduri este:

2.Suma gradelor tuturor nodurilor unui graf neorientat este egala cu dublul numarului de muchii.

3.Daca graful G neorientat are n noduri, n>2, atunci cel putin 2 noduri au acelasi grad.
4.Pentru orice grad neorientat numarul nodurilor de grad impar este par.
5.Numarul minim de muchii pe care trebuie sa le aiba un graf neorientat cu n noduri, ca sa nu existe noduri izolate este:
Se numeste lant intr-un graf neorientat o succesiune de varfuri cu proprietatea ca intre oricare doua varfuri(noduri) alaturate exista o muchie.
Numim lant elementar o succesiune de varfuri care respecta proprietatea de lant si-n care oricare doua varfuri sunt distincte. In caz contrar lantul se numeste neelementar.
Lungimea unui lant reprezinta numarul de muchii/arce din care este format.
- Lantul simplu este lantul care contine numai muchii/arce distincte.
- Lantul compus este lantul care nu este format din muchii/arce distincte.
- Lantul elementar este lantul care contine numai noduri distincte.
Ciclu elementar este un ciclu in care toate nodurile sunt distincte doua cate doua (cu exceptia primului si ultimului nod).
Numim ciclu un lant in care toate muchiile/arcele sunt distincte doua cate doua si primul nod coincide cu ultimul.
Un graf fara cicluri se numeste graf aciclic.
Se numeste graf partial notat cu Gp=(x,v), cu proprietatea ca multimea v de perechi de varfuri este inclusa in multimea x.
Imaginea 1 prezinta un graf oarecare iar imaginea 2 prezinta graful partial al primului prin eliminarea muchilor (1,2) si (2,4).