Graf complet
Definitie
Fie G = (V, M) un graf neorientat. Graful G se numeste graf complet daca oricare doua varfuri distincte ale sale sunt adiacente.
Observatii:
- Graful complet se noteaza cu Kn (n reprezinta numarul de noduri)
- d(i) = n-1
- intr-un graf Kn exista n(n-1)/2 muchii
Observatii:
- Graful complet se noteaza cu Kn (n reprezinta numarul de noduri)
- d(i) = n-1
- intr-un graf Kn exista n(n-1)/2 muchii
EXEMPLU:
Graful Bipartit
Definitie:
Un graf G=(X,U) se numeste graf bipartit daca exista 2 multimi nevide A si B astfel incat X= AB si AB=∪∩φ si oricare muchie din U a lu G are o extremitate in A si una in B.
EXEMPLU:
G=(X,U)
X={1,2,3,4,5,6,7}
U={[1,2];[1,5];[3,5];[3,6];[4,7]}
A={1,3,4}
B={2,5,6,7}
Observatie:
1) Un graf bipartit se numeste complet daca pentru oricare x din A si oricare y din B exista muchia xy.
2) Daca A are p elemente, iar B are q elemente, numarul total de muchii ale unui graf bipariti este p*q.

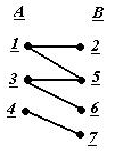
Niciun comentariu:
Trimiteți un comentariu